This article is mentioned in:

Introduction

Brown-Séquard syndrome (BSS) is a syndrome consisting of ipsilateral upper motor neuron paralysis (hemiplegia) and loss of proprioception with contralateral pain and temperature sensation deficit. BSS is usually observed in association with traumatic spinal cord injuries, extramedullary spinal cord tumors, spinal hemorrhages, degenerative disease and infectious and inflammatory causes, including multiple sclerosis (1). There have also been a few reports of BSS associated with intradural spinal cord herniation or disc herniation (2,3). Furthermore, complete BSS due to chronic compression is rare and most patients present with an incomplete form of this condition (4).

In the present study, a 3-dimensional finite element method (3D-FEM) was used to analyze the stress distribution of the spinal cord under various compression levels corresponding to five different lengths of the transverse diameter. Three levels of static compression corresponding to 10, 20 and 30% of the anteroposterior (AP) diameter were used for each of these five conditions. This model was used to investigate why the number of cases of complete BSS resulting from chronic compression is limited.

Materials and methods

Construction of the 3D-FEM spinal cord model

The Abaqus 6.11 (Dassault Systèmes Simulia Corp., Providence, RI, USA) standard finite element package was used for FEM simulation. The 3D-FEM spinal cord model used in this study consisted of gray and white matter and pia mater. In order to simplify calculation in the model, the denticulate ligament, dura and nerve root sheaths were not included. Pia mater was included since it has been demonstrated that spinal cord with and without this component shows significantly different mechanical behaviors (5). The spinal cord was assumed to be symmetrical about the mid-sagittal plane, so that only half the spinal cord required reconstruction and the whole model could be integrated by mirror image. This model simulated chronic compression of the cervical spinal cord. The vertebral canal model consisting of lamina was established by measuring 13 cervical computed tomographic myelographs (Fig. 1). A rigid flat plate was used as a compression factor from the anterior surface of the spinal cord and its width was 25, 37.5, 50, 62.5 and 75% of the length of the transverse diameter of the spinal cord (Fig. 2). The rigid flat plate was located at the longitudinal center of the spinal cord. The spinal cord consists of three distinct materials: the white and gray matter and the pia mater. The mechanical properties (Young’s modulus and Poisson’s ratio) of the gray and white matter were determined using data obtained from the tensile stress strain curve and stress relaxation tests under various strain rates (6,7). The mechanical properties of the pia mater were obtained from a previous study (8). The mechanical properties of the lamina and flat plate were stiff enough to enable the spinal cord to be pressed. Based on the assumption that no slippage occurs at the interfaces of white and gray matter and pia mater, these interfaces were glued together. Data concerning the friction coefficient between the bone and spinal cord were not available. The coefficient of friction between lamina and the spinal cord was ‘glue’ at the contact line and ‘frictionless’ next to the part in contact. Similarly, the coefficient of friction between the rigid flat plate and spinal cord was ‘glue’ at the contact interfaces and ‘frictionless’ next to the part in contact. To simulate the axial injury model of the spinal cord, nodes at the bottom and top of the spinal cord model were constrained in all directions. The spinal cord and the rigid flat plate were symmetrically meshed with 20-node elements. With a FEM model of 50% of the length of the transverse diameter of the spinal cord, the total number of isoparametric 20-node elements was 12,535 and the total number of nodes was 76,993.

Figure 1. Three-dimensional finite element method (3D-FEM) model of the spinal cord and the vertebral canal model consisting of lamina.

Figure 2. The rigid flat plate applied compression to 25, 37.5, 50, 62.5 and 75% of the length of the transverse diameter of the spinal cord.

Static compression model

For the simulation of BSS, anterior static compression was applied to the spinal cord by the rigid flat plate at 25, 37.5, 50, 62.5 and 75% of the length of the transverse diameter of the spinal cord. The degrees of compression were 10, 20 and 30% of the AP diameter of the spinal cord. A 10% compression was first applied to the spinal cord, followed by compressions of 20 and 30%. In total, 15 different compression combinations were evaluated.

Results

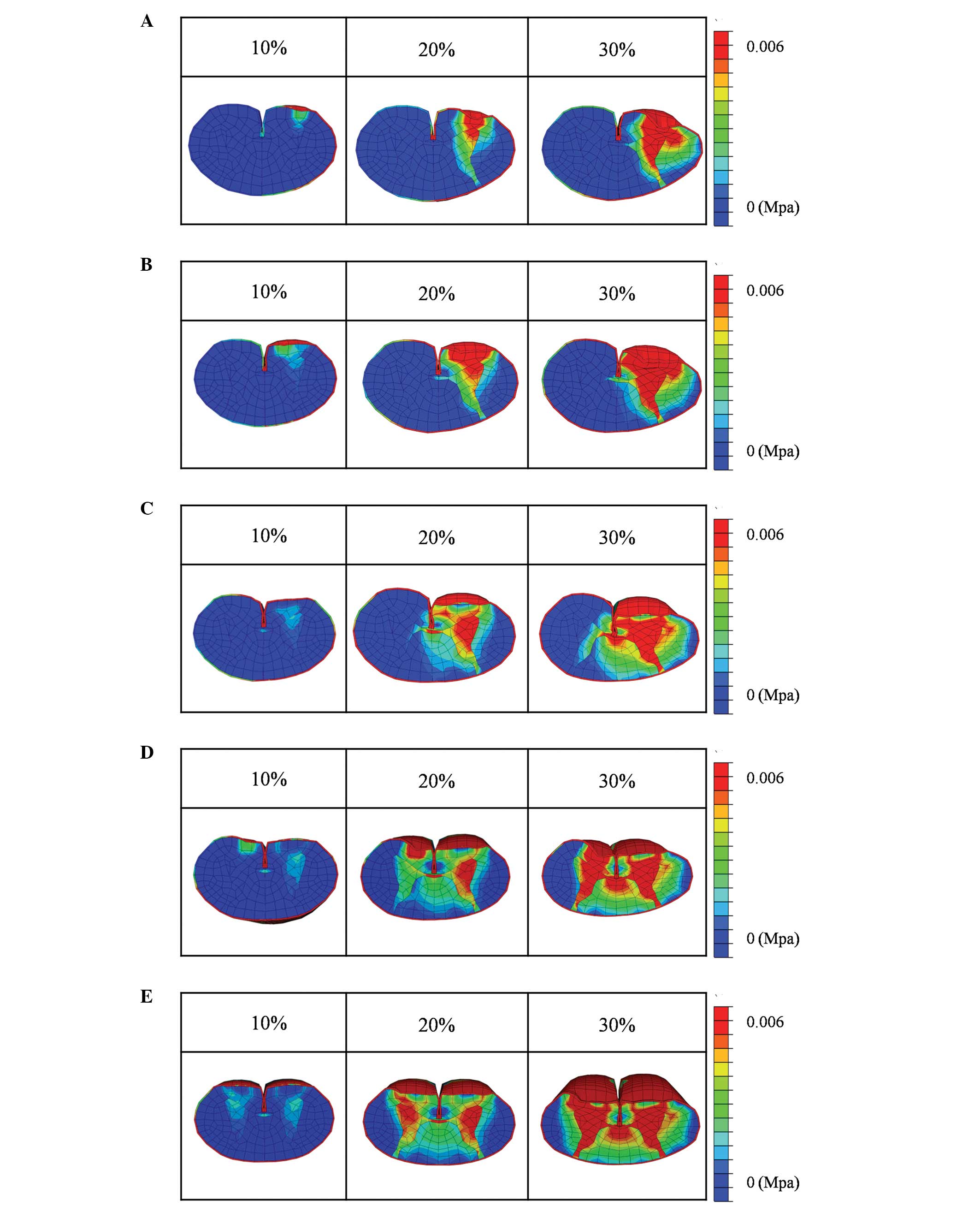
Under compression of 25% of the length of the transverse diameter of the spinal cord with a rigid flat plate, the stresses were extremely low when the degree of compression was 10% of the AP diameter of the spinal cord. The stress was confined to part of the gray matter and to the anterior funiculus. At 20% compression, the stress on the anterior horn and part of the anterior funiculus was slightly increased. At 30% compression, high stresses were observed in the gray matter, anterior funiculus and part of the lateral funiculus, but not the posterior funiculus (Fig. 3A).

Figure 3. Static compression corresponding to 10, 20 and 30% of the anteropostrior (AP) diameter of the spinal cord was applied by compression of (A) 25, (B) 37.5, (C) 50, (D) 62.5 and (E) 75% of the length of the transverse diameter of the spinal cord with a rigid flat plate.

Compression of 37.5% of the length of the transverse diameter of the spinal cord with a rigid flat plate resulted in stresses that were very low when the compression of the AP diameter of the spinal cord was 10%. The stresses on the gray matter and anterior funiculus were slightly increased when 20% compression was applied. At 30% compression, high stresses were observed in the gray matter, anterior funiculus and lateral funiculus, while the stress was moderately increased in part of the posterior funiculus (Fig. 3B).

When 50% of the length of the transverse diameter of the spinal cord was compressed with a rigid flat plate, the stress was very low when the degree of compression was 10% of the AP diameter of the spinal cord, and was observed only in the gray matter and part of the anterior funiculus. At 20% compression, the stress on the gray matter and anterior funiculus was slightly increased. At 30% compression, the stress on the spinal cord was increased and high stresses were observed in the gray matter and the anterior, lateral and posterior funiculi. However, the stress was not increased on the posterior funiculus of the non-compressed side (Fig. 3C).

A compression of 62.5% of the length of the transverse diameter of the spinal cord with a rigid flat plate resulted in very low stresses when the degree of compression was 10% of the AP diameter of the spinal cord; the stress was only slightly increased in both anterior funiculi. At 20% compression, the stress increased in the gray matter and the anterior funiculus on the compressed side. At 30% compression, the stress on the spinal cord was increased and high stresses were observed in the gray matter and anterior funiculi of both sides, the lateral funiculus of the compressed side and both posterior funiculi. The stress was not increased in the lateral funiculus of the non-compressed side (Fig. 3D).

Under compression of 75% of the length of the transverse diameter of the spinal cord with a rigid flat plate, the stress on the spinal cord was very low at 10% compression of the AP diameter of the spinal cord. At 20% compression, the stress increased in the gray matter and anterior funiculi of both sides. At 30% compression, the stress on the spinal cord was increased and high levels of stress were observed in the gray matter of both sides, as well as in the anterior, lateral and posterior funiculi of both sides (Fig. 3E).

Discussion

BSS was first described by Brown-Séquard in a study of a patient who was suffering from a knife injury and who presented with hemicord syndrome (9). BSS involves ipsilateral loss of motor function resulting from corticospinal tract interruption, combined with a contralateral loss of pain and temperature sensation as a result of spinothalamic tract dysfunction. BSS is most often observed in association with traumatic injuries to the spinal cord (10–12). The incidence of complete BSS due to chronic compression is very low. In one study, complete BSS was observed in 4.6% of 600 cases reported as BSS (4) and these comprised trauma (1.0%), tumoral compression (0.8%) and non-tumoral compression or non-compressive lesions (2.8%). The contribution of cervical disc herniation to BSS has been estimated by Jomin et al (13) to be 2.6%, but no further details were provided in this study. Choi et al (14) reported that only five of the 2,350 cases (0.21%) in their series were retrospectively evaluated as complete BSS caused by cervical disc herniation. Nine percent of the patients who presented with symptoms of thoracic disc herniation were diagnosed with BSS (15), but this study did not classify cases into complete or incomplete BSS. BSS may also constitute the initial symptom for idiopathic spinal cord herniation (ISCH), a rare cause of progressive myelopathy (16–19). ISCH is characterized by spontaneous herniation of the spinal cord through an anterior or antero-lateral dural defect. A review of the literature relevant to ISCH showed that 73/100 reported cases (73%) presented with BSS, 19 (19%) with spasticity and eight (8%) with numbness or leg pain (20) However, this study did not provide details concerning whether the BSS was complete or incomplete.

Based on these previous findings, we hypothesized that pressure within a limited range of compression causes complete BSS with static compression. To test this hypothesis, we investigated three different degrees of static compression under five different compressions of the transverse diameter of the spinal cord. We calculated the stress distributions inside the spinal cord and simulated complete and incomplete BSS using a 3D-FEM model.

The aim of the present study was to develop a 3D-FEM spinal cord model that simulates the clinical situation. In a similar manner to previous studies by Kato et al (21–23), Li et al (24,25) and Nishida et al (26,27), bovine spinal cord or magnetic resonance imaging (MRI) was used in the model for the present analysis since it was not possible to obtain fresh human spinal cord. The mechanical properties of the spinal cord used in the present study were similar to those reported in earlier studies (6–8). Li and Dai (24) noted that it was reasonable to make use of the mechanical properties of bovine spinal cord since the brains and spinal cords of cattle and humans exhibit similar changes when injured. In the present study, we also assumed that the mechanical properties of the spinal cords from the two species were similar. Persson et al (5) described the division of spinal cord into pia mater and white and gray matter, and demonstrated that the presence of pia mater had a significant effect on spinal cord deformation; thus, pia mater is required to simulate the clinical situation effectively.

The present study was limited to the investigation of stress distribution caused by compression. Additional casual factors that may contribute to cervical spondylotic myelopathy (CSM) include ischemia, congestion and spinal cord stretch injury (28). Blood flow was not analyzed in this FEM analysis and only one movement (static compression) was investigated for potential association with BSS. Long-term compression and apoptotic factors were not considered in this FEM analysis. Moreover, the FEM model used in the present study was simplified in order to facilitate the calculations. Analysis errors were reduced by using a FEM mesh, assuming the spinal cord was symmetric, not including the denticulate ligament, dura and nerve root sheaths, and setting a close distance between the spinal cord and lamina, spinal cord and anterior compression of the spinal cord.

When the rigid-flat-plate compression was applied to <37.5% of the length of the transverse diameter of spinal cord, the stress on the gray matter, anterior funiculus and lateral funiculus was increased, but not the stress on the posterior funiculus. Consequently, contralateral loss of pain, temperature sensation and ipsilateral loss of motor function are likely to occur, but not ipsilateral disorders of vibration and position sense. This may correspond to cases of incomplete BSS.

When the rigid-flat-plate compression was applied to >62.5% of the length of the transverse diameter of the spinal cord, the stress increased on the gray matter, the anterior funiculi and the posterior funiculi on both sides and on the lateral funiculus on the compression side, but not the lateral funiculus on the non-compression side. Based on these results, the loss of pain and temperature sensation, as well as ipsilateral loss of motor function on the compression side are expected to occur. Disorders of vibration and position sense are also likely to occur and, thus, this situation may correspond to cases with incomplete BSS.

Under a rigid-flat-plate compression of 50% of the length of the transverse diameter of the spinal cord and compression of 10% of the AP diameter of the spinal cord, the stress levels in the gray matter were very low. At 20% compression, the stress levels were slightly increased in the gray matter and anterior funiculus, while at 30% compression, the levels of stress were increased in the gray matter, as well as in the anterior, lateral and posterior funiculi. This may result in the contralateral loss of pain and temperature sensation due to anterior funiculus compression, ipsilateral loss of motor function due to lateral funiculus compression, and ipsilateral disorders of vibration and position sense due to posterior funiculus compression. However, the distribution of stress to the posterior funiculus of the non-compressed side and was not observed; thus, this may correspond to cases of complete BSS.

The simulation model used in the present study showed that only at a compression of 50% of the length of the transverse diameter of the spinal cord did the stress distribution lead to complete BSS. However, compression within such a limited range is an infrequent clinical event and, thus, this may explain why the number of cases of complete BSS associated with chronic compression is rare.

References