This article is mentioned in:

Introduction

Micro-finite element (µFE) models, created from high resolution micro-computed tomography (µ-CT) images, have become a major computational tool for the assessment of the mechanical properties of human trabecular bone. By simulating a loading condition, this model then can be used to simulate the mechanical behavior of trabecular bone (1,2), and has shown excellent prediction power compared with experimental measurements (3,4). µFE analysis, based on this model, is potentially useful when evaluating the effects of bone diseases and their subsequent treatment on the mechanical properties of trabecular bone.

To date, µFE models of trabecular bone have predominantly been based on cored samples extracted from sites with high concentrations of the trabecular bone, for example, the vertebral body or proximal part of femur (5,6). Among the studies using µFE models, the shapes of µFE models are typically cubical and cylinder. Gross et al (6) constructed cubic µFE models within the vertebral body in their study to investigate morphology-elasticity relationships. Cubic µFE models with a side length of 4 mm within the vertebral body were set to obtain the biomechanical properties of human trabecular bone (7). Cylindrical trabecular µFE models were also constructed to investigate the mechanical properties of vertebral trabecular bone (3,8).

To the best of our knowledge, whether there are differences between cubic and cylindrical µFE models has not yet been studied. Therefore, the purpose of our study was to investigate the influence of the shape of the µFE model on the mechanical properties calculated from µFE analysis, and to determine whether there were differences between cubic and cylindrical µFE models.

Materials and methods

Specimens preparation

In total, 5 lumbar vertebral bodies (L1-5) were collected form one embalmed human cadaver (61 years old; male) provided by the Department of Human Anatomy at the Fourth Military Medical University (Xi'an, China). Written informed consent from the donor was obtained for the use of these specimens in research. Collection and preparation procedures were approved by the Ethics Committee of the Fourth Military Medical University. All specimens were physically evaluated and radiographed to exclude bone diseases, bone cancers, and previous fractures. Soft tissues were carefully removed from the bone with a scalpel. Lateral and posterior elements including the pedicle, transverse process, and spinous process were excised from the vertebral body using a band saw (Isomet 1000, Buehler, Plymouth, MN, USA).

µ-CT scanning. µ-CT scans of all samples (5 vertebral bodies) were performed with a high-resolution µ-CT system (Siemens Inveon; Siemens AG, Munich, Germany) with an isotropic resolution of 33.355 µm. Image processing included the application of a modest Gauss global filter and segmentation according to the method described by Otsu (9), which is a popular and established method in the field of threshold segmentation. Images were obtained using the following parameters: i) X-ray tube voltage, 100 kV; ii) anode current, 100 µA; and iii) shutter speed, 2,500 msec. High resolution images were obtained to produce µFE models for subsequent studies.

µFE model building

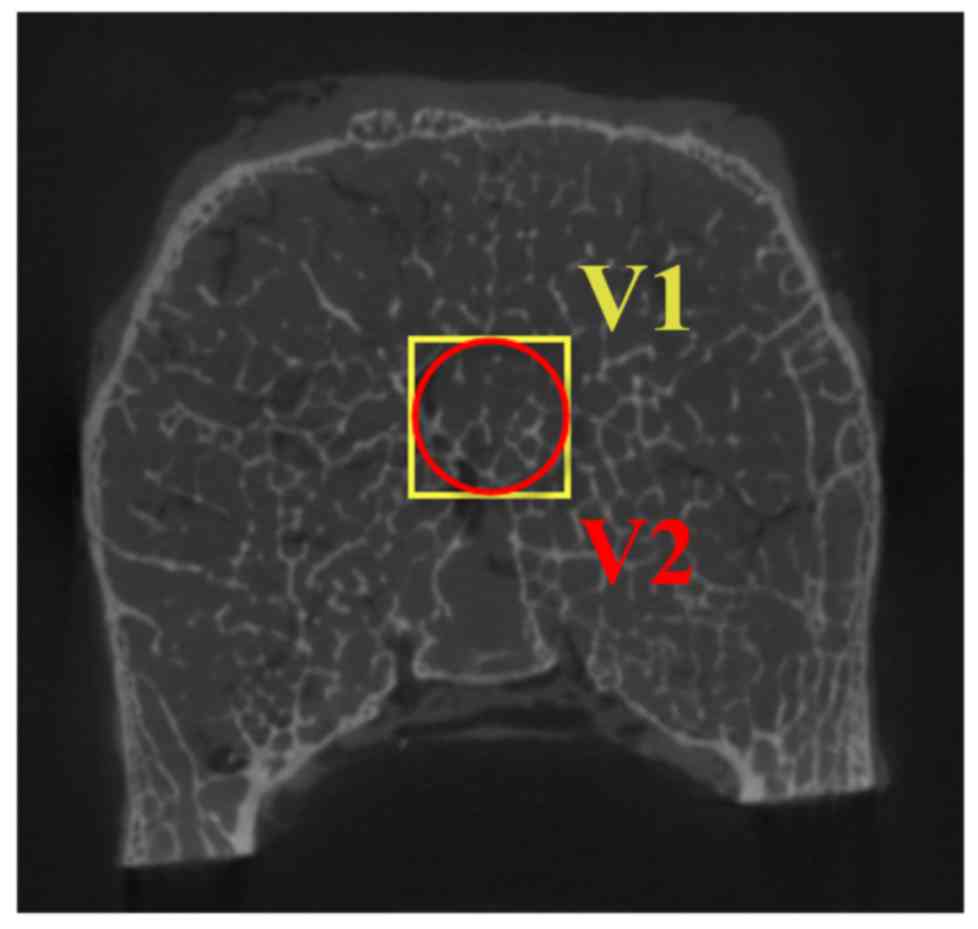
µFE models were generated directly from the segmented images using a voxel conversion process (10). Firstly, all the DICOM image files were imported into the ScanIP software package (version 3.2; Build 1, Simpleware Ltd., Exeter, UK) to crop the different volumes of interest (VOI). As shown in Fig. 1, cubic cores (V1 in Fig. 1) of 8×8×8 mm3 were cropped to build cubic µFE models. Inscribed cylindrical cores (V2 in Fig. 1) of 8-mm diameter and 8-mm height were cropped to build cylindrical µFE models. Images were then segmented with the optimal threshold to match the bone volume fraction measured from µ-CT analysis. The Floodfill function in the ScanIP software was used to remove all the floating or disconnected structures. Two layers of voxel elements were added at the superior and inferior surface to mimic stainless steel layers in axial compression tests.

Figure 1. VOI in the vertebral body. Cubic VOI is shown as V1 in yellow color, and inscribed cylindrical VOI is shown as V2 in red color. VOI, volume of interest.

Subsequently, the files were imported into ScanFE (version 3.1.2, Build 2, Simpleware Ltd., Exeter, UK) to construct the µFE model. With this approach, voxels representing bone tissue were converted to equally sized eight-node hexahedral voxel elements, whereas voxels representing the bone marrow were ignored. All the models were imported to ANSYS (release 14.0; ANSYS, Inc., Township, PA, USA) to perform further calculations. For all models, the element material properties of bone were considered to be isotropic, linear elastic, and uniform with a tissue Young's modulus of 10 GPa and a tissue Poisson's ratio of 0.3 (11). An isotropic homogenous tissue modulus of 200 GPa and a tissue Poisson's ratio of 0.3 was assigned to the element of stainless steel layers (12).

Computational process of µFE analysis

A 1% axial strain was prescribed to the top surface of the model, and axial displacements at the bottom surface were constrained, simulating an axial compression test along the superior-inferior direction. Contact between the upper and lower surfaces of the specimen and the steel plates were modeled using contact elements with a zero friction value to ensure that only compressive forces were transmitted (13). All analyses were performed on a workstation computer (ThinkStation; Intel Xeon CPU E3-122, 3.10 GHz, Lenovo Group Ltd., Beijing, China). The apparent stresses were calculated as the total reaction force per apparent area. Based on that, the E values were calculated by dividing the apparent strain by 0.01 (14).

Statistical analysis

Statistical analyses were performed using the SigmaPlot 12.5 (Systat Software Inc., San Jose, CA, USA). Paired-t tests were performed to determine whether there were differences between the E values obtained from cubic and cylindrical models. P<0.05 was considered to indicate a statistically significant difference.

Results

Von Mises stress distributions

Von Mises stress distributions in the trabecular bone structure of cubic and cylindrical µFE models are shown in Fig. 2. There were no significant differences of Von Mises stress distributions between cubic and cylindrical µFE models.

Figure 2. Von Mises stress distribution in the trabecular bone structure of cubic and cylindrical µFE models. (A) Cubic µFE models and (B) cylindrical µFE models. µFE, micro-finite element.

E values

E values obtained from µFE analyses are shown in Fig. 3. E of the cubic models was 146.34±9.76 MPa, and of cylindrical models was 139.35±13.21 MPa. Paired t-tests showed that there were no statistically significant differences in E values between the cubic and cylindrical models.

Figure 3. E values calculated from cubic and cylindrical models. Paired t-test demonstrated that there were no significant differences between these two models. Data are presented as the mean ± standard deviation.

Discussion

In the present study, cubic and cylindrical µFE models were built to investigate if there were significant differences between these two models. No significant differences in the E values were detected between the cubic and cylindrical µFE models.

µFE analysis is now widely used to investigate bone mechanical properties; these mechanical properties have been demonstrated to relate to bone microarchitecture (15). Based on high resolution 3D images obtained from µCT, µFE models were constructed for further simulation calculations. By simulating a loading condition, this model can be used to derive the elastic modulus of the bone, as well as the distribution of stresses and strains in the bone tissue (1,16).

Obtained from µFE models, trabecular bone modulus has a good correlation with experimental modulus and strength (15,17). Elastic modulus obtained in our studies were similar to former experimental compression studies on trabecular bone samples (18,19). Compression tests on vertebral trabecular bone cores have shown that the apparent elastic modulus on axial direction was 189.7 MPa (18), which is simular to the value of 139.96–146.34 MPa obtained in the present study. In another study based on vertebral trabecular bone, apparent elastic modulus calculated from µFE models was 146–154 MPa (19). These findings indicated that the µFE models constructed in our study are reliable.

Voxels representing bone tissue were converted to equally sized eight-node hexahedral voxel elements to construct µFE models in our study. A number of studies have investigated the effect of voxel size on the accuracy of biomechanical measurements on human trabecular bone (20–22). Voxel size predominantly refers to scanning and reconstruction voxel size. Scanning voxel size is based on the µ-CT scanning resolution. A previous study demonstrated that it is the resolution of raw data that primarily determines the accuracy of models as the bone volume fraction of bone volume/total volume was predominantly affected by the scanning resolution (22). The scanning resolution of the µ-CT system used in our study was 33.355 µm, which was enough to depict the microarchitecture of human trabecular bone (23,24). In another study, the recommended resolution in finite element models of trabecular bone was one quarter of trabecular thickness (25). The thickness of trabeculae in our study was ~200 µm and the resolution of 33.355 µm, fulfilling the conditions rule. Reconstruction voxel size is the actual voxel size concerted to the 3D µFE model. The reconstruction voxel size in our study was identical with scanning voxel size, and this could avoid the inaccuracy of coarsening reconstruction voxel size.

The size of cubic and cylindrical models in our study has contained enough structural information for virtual compressions. Pahr and Zysset (26) suggested that the side length of the volume should be >5 mm as it may provide the proposed boundary conditions. Another study showed that the VOI of trabecular bone should be >6×6×6 mm3 to predict the microarchitecture of human trabecular bone (27). The VOI of trabecular bone in our study met these conditions. The µFE models constructed in our study included a representation of steel plate located on the upper and lower surfaces of the specimen. The lower steel plate was constrained and compressive displacement was applied to the upper steel plate. All these conditions stimulated the experimental compression test better.

Notably, the cubic and cylindrical µFE models were constructed from the same position of the vertebral body. It has been confirmed that the architecture of the trabecular bone within the vertebral body is inhomogeneous (17,28–31). Within the vertebral body, the trabecular architecture in the posterior region was superior to the anterior region (28,31). Compared with the posterior region, the anterior region had lower bone mass density, less trabecular bone volume fraction, less trabecular number, and greater trabecular separation (28). Although there were no significant differences between cubic and cylindrical µFE models, the positions of the trabecular bone core should be identical.

In experimental compression tests, trabecular bone cores extracted from vertebral bodies are often used (23,32). In our study, cubic and cylindrical µFE models were constructed to investigate if there were differences between the two models. This indicated that the shape of trabecular bone core used in experimental biomechanical tests may not affect the biomechanical properties obtained from these real tests. These computational models used in our study may enable us to make repeated virtual compression tests on trabecular bone core extracted from the same specimen. This may avoid the influence of variance among different specimens and ensure the results are more reliable.

To construct µFE models of trabecular bone, choosing the VOI was critical. Cubic and cylindrical VOI are the most commonly used shapes of VOI (3,33). The results demonstrated that there was no significant difference between these two models. With regard to the Von Mises stress distributions, there were also no significant differences between cubic and cylindrical µFE models. Choosing between the cubic or cylindrical models shall depend on the specific study design. A limitation of the present study was that the trabecular bone specimens used in our study were collected from vertebral bodies. It has is well-documented that the morphologies of trabecular bone harvested from different skeletal sites are quite different (34,35). Further research is required to confirm that the findings of the present study are applicable to other skeletal sites.

In conclusion, to construct µFE models of vertebral trabecular bone, cubic or cylindrical models were both feasible. The present findings demonstrated that there were no significant difference between these two shapes of models. To choose cubic or cylindrical model, it depends on the specific study design.

Acknowledgements

The authors would like to thank Jia-Ji Yang at the School of Stomatology of Fourth Military Medical University for their technical assistance at µCT analysis. This study was supported by the National Nature Science Foundation of China (grant no. 81301292).

References