This article is mentioned in:

Introduction

Lung cancer (LC) is a leading cause of cancer-associated mortalities worldwide. Histologically, LC is stratified into two categories, small cell lung cancer (SCLC) and non-small cell lung cancer (NSCLC), of which the latter is more prevalent (1). NSCLC can be further classified into three major subtypes, where adenocarcinoma (AC) and squamous cell carcinoma (SCC) together account for ~70% of the total cases of LC (2). Since AC and SCC differ in cell of origin, location within the lung, growth pattern and molecular mechanisms, they are regarded as two distinct diseases (3). Until recently, however, NSCLC subtypes had been typically treated with same therapeutic approaches (1). Apart from a lack of timely detection of tumors, the administration of homogenous treatments to NSCLC patients regardless of the histology subtypes might account for why no substantial improvement in the 5-year survival rate of patients with NSCLC has been made over the years (3,4). Therefore, more ‘personalized’ therapeutic strategies for AC and SCC patients are highly desirable, which necessitates the identification of subtype-specific prognostic molecular markers for AC and SCC.

Feature selection or variable selection, which aims at selecting a gene signature (subset) among thousands of genes with objectives, including diagnosis of diseases, segmentation of disease subtypes and drug response or survival prediction for patients, is currently becoming a routine practice in bioinformatics (5,6). Regarding NSCLC, extensive efforts have been devoted to distinguishing AC from SCC and also to distinguish patients with good prognosis from those with poor prognosis with the aid of feature selection algorithms (3,7–11). Compared with the diagnosis task or the classification task, it has been demonstrated that the prognosis task is more difficult to accomplish (12,13). Furthermore, the present study focused on subtype-specific prognosis, with extra consideration on subtype information to introduce more complexity to statistical modeling. Subtype-specific prognostic genes may be identified by either separate application of a feature selection method to each subtype or by a modification of an existing method to enable the identification of subtype-specific prognostic genes (14). Compared with a separate modeling method where feature selection algorithms that can handle survival data (LASSO method and random forest method) was implemented on each subtype, a natural extension is more theoretically sound but accompanied with extra statistical complexity (15). The two feature selection algorithms, the Cox filter method and the Cox-Threshold Gradient Descent Regularization (Cox-TGDR) method (15,16), belong to the natural extension category. (Both the Cox filter method and the Cox-TGDR method were proposed by the authors). These two methods are all based on the seminal model of survival analysis: A Cox regression model (17).

Gene expression profiles contain grouping structure with genes inside each group that are highly correlated and therefore more likely to co-function together to affect biological processes (18,19). However, both the Cox filter method and the Cox-TGDR method are typical gene-based feature selection methods where the underlying grouping structure is ignored (20). By contrast, a pathway-based feature selection method incorporates the grouping structure either explicitly or implicitly to guide the selection of relevant genes (21). Many studies have demonstrated that a pathway-based feature selection method is usually superior to its gene-based counterpart in terms of predictive capacity, model stability and biological interpretation (21–25).

Furthermore, a failure to account for the correlations among genes may result in many ‘redundant’ genes being included, and therefore an increase in the false positive rate. As the Cox filter method screens the relevant genes individually (see the Materials and Methods section for details), it has no control over the false positive rate. The simulations conducted in previous studies (15,16) have justified this point. Until the drawback of false positive rate is fully addressed, the widespread application of the Cox filter method remains challenging.

In this article, the Cox filter method was extended so that the resulting extension not only accounts for the interactions/dependency among genes but also eliminates many redundant genes. The GeneRank method (26) was employed to pre-filter genes and subsequently average correlation coefficients were calculated to determine the correlation of a specific gene with other genes in the search space. Given that the GeneRank method was also used to pre-filter genes in a previous study by the present authors (14), these two studies have some similarities. Nevertheless, the objectives of the studies differ dramatically. The aim of the previous study (14) was to illustrate that for different outcomes of interest (e.g., segmentation of different subtypes versus predicted survival time), the corresponding relevant genes differ and therefore a supervised learning method is preferred over an unsupervised method. By contrast, the present study focuses on the identification of subtype-specific gene signatures.

After the proposed procedure was applied to the NSCLC gene expression data and compared with several relevant algorithms, whether the proposed procedure can identify gene signatures with better predictive performance and more meaningful biological implication than other methods was determined.

Materials and methods

Experimental data

The microarray data included GSE30219, GSE37745 and GSE50081 datasets, which were publicly assessable from the Gene Expression Omnibus (GEO, https://www.ncbi.nlm.nih.gov/geo/) repository. The inclusion criteria were: i) Being profiled on the Affymetrix HG-U133 Plus 2.0 platform; ii) inclusion of AC and SCC subtypes; iii) inclusion of early pathological stages (stage I or II); iv) no administration of adjuvant therapy to patients; and v) availability of the raw data so that the same pre-processing procedure was used to obtain the gene expression values. There were 85 AC and 21 SCC patients, 40 AC and 24 SCC patients, 127 AC and 42 SCC patients in GSE30219, GSE37745 and GSE50081, respectively. In total, there were 339 patients in the integrated dataset that combined these three datasets together, which served as the training set in the present study.

The RNA-Seq data were downloaded from The Cancer Genome Atlas Data Portal (level 3) (https://tcga-data.nci.nih.gov/tcga/). The cohorts that were considered are: LUAD for AC subtype and LUSC for SCC subtype. By restricting the patients to those at early stages of disease, not undergone any adjuvant treatment and where survival information was available, 70 AC and 55 SCC patients were included.

Pre-processing procedures

Raw data (CEL files) of the microarray data sets were downloaded from the GEO repository. The expression values were obtained using the fRMA algorithm (27) and were normalized using quantile normalization separately for each experiment. Then, the expression values of these three studies were combined together and the COMBAT algorithm (28) was used to eliminate the potential batch effects. The resulting data served as the training set and were referred to as the integrated dataset.

Counts-per-million (CPM) values for the RNA-seq data were calculated and log2 transformed by Voom function (29) in R limma package (30). The RNA-seq data were used as the test set to validate the performance of resulting prognostic signatures. There were 14,573 unique genes annotated by both the microarray data and the RNA-seq data. The protein-to-protein interaction information was retrieved from the Human Protein Reference Database (HPRD, http://www.hprd.org). There were 9,672 protein-coding genes annotated by the HPRD database (Release 9). The downstream analysis was carried out using the overlapped 8,023 genes annotated by the microarray data, the RNA-seq data and the HPRD database. Compared with a previous study by the authors, the training set and the total genes under consideration were different in the present study. Specifically, the data from GSE50081 experiment were used to train the prognostic signatures, and a number of pre-filtering steps were performed to downsize the number of genes under consideration in the microarray data to 6,202 (16).

Statistical methods

Cox filter method. The Cox filter method (16) was used to identify genes that were informative of survival rate for AC/SCC histology subtypes. In this method, each gene was fit with a Cox model. The hazard function of patient i for gene g (g=1,…,p) is given by:

where, Xij=(Xij1,…,Xijp)T represents the actual expression values for the p genes under consideration and λ0g(t) is an unknown baseline hazard function. I (j=SCC) is an indicator, it takes the value of 1 if the histology subtype j of patient i is SCC or otherwise the value of 0. The values of βACg (i.e., β2g) and βSCCg (i.e., β2g+β3g) determine if subtype-specific prognostic genes exist. Specifically, βACg≠0 but βSCCg=0 corresponds to an AC-specific gene while βSCCg≠0 but βACg=0 corresponds to an SCC-specific gene.

GeneRank

The GeneRank method (26) calculates ranks for genes by accounting for both the gene expression values and the connectivity information among them. Firstly, according to whether a connection is recorded between genes in the HPRD database, a pxp adjacency matrix was made (here, p is the number of genes under consideration) whose ijth and jith components are 1 if gene i and gene j are connected, 0 otherwise. Then, the GeneRank method solves the following equation:

where W stands for the adjacency matrix of genes, and D is a diagonal matrix, where diagonal components record the number of genes that a specific gene is connected to in the gene network graph. The gene expression value is represented by exp. In the GeneRank method, d is a tuning parameter, balancing the effect of the expression value of a gene and its level of importance inside the whole gene-to-gene interaction network. The gene expression values only determine the ranks of the genes when d equals to 0. On the other hand, the GeneRanks depend completely on the connectivity level of genes when d=1. The default value of d is 0.5.

In the present study, the ranks generated by the GeneRank method were used to rearrange genes in the ascending order and then the search domain was restricted to the top ranked genes in the resulting list. With this filter, the least important genes in both pathway connectivity and expression difference were ruled out.

Redundant gene elimination

To eliminate the redundant genes, which are highly correlated with the true causal genes and therefore tend to be also selected by a feature selection algorithm, particularly a filter method, a method proposed previously (31) was adopted to account for the correlation coefficients between genes during the filtering process. Specifically, the average correlation coefficient between a candidate gene g and other genes in the restricted search space was calculated as follows:

where, |cor(g.j)| represents the absolute value of Pearson's correlation coefficient (PCC) between gene g and gene j, and |S| is the total number of genes in the search space. Then, a gene is regarded to be relevant if it fits two conditions: i) its corresponding adjusted P-values of the Cox filter model are <0.05. (The BH procedure was used to adjust for multiple comparison problem); and ii) its average absolute correlation coefficients in the search space are <0.2. With the second restriction, i.e., the restriction on the average PCC value of a gene, some control over the redundant genes is provided. Originally, a new statistic was defined that multiplied the adjusted P-value by corgs for gene g, and this was used to determine the significance level of genes. The newly defined statistic was named as RRP (P-value with redundant gene removal). However, it is realized that RRP has some fatal drawbacks. For instance, if the PCCs of a gene with other genes in the search space are all close to 0, then its RRP is extremely small although the P-value in the Cox filter model for this specific gene is 1. As a result, the RRP statistic had been overruled.

Sign average

A regression model would become non-identifiable when the number of covariates exceeds the number of samples. To avoid this, the risk profile of a patient was summarized as the sign average (13,32) of the expression values over all selected genes. Specifically for each subtype, all genes inside the selected gene subset, i.e., the AC-specific and SCC-specific prognostic genes are stratified into either the hazardous group H or the preventive group P according to the signs of their estimated effects in the Cox filter method, i.e., β2g for AC and β2g+β3g for SCC. In the hazardous group, the genes for which increased expression is associated with a higher hazard are included. Conversely, the genes for which an increment in expression is associated with a lower hazard of mortality are put in the preventive group. Of note, there are two sets of notations, i.e., HAC in which β2g >0 and PAC in which β2g <0 for AC patients, and HSCC in which β2g+β3g >0 and PSCC in which β2g+β3g <0 for SCC patients in the present study. Denoting the number of genes inside the gene set GS as |GS|, the sign average for AC patient i(i=1,…, n1) and SCC patient j (j= n1+1,…, n) is defined respectively as:

Statistical metrics

The first metric used to evaluate the performance of a resulting prognostic gene signature is the censoring-adjusted C-statistic (33) over the follow-up period (0, τ). It is defined as:

where g(X) is the risk score for a subject with predictor vector X. Although a value of 0.5 for the C-index corresponds to the random guess model, a moderate value in between 0.6–0.7 already indicates a satisfactory performance as discussed previously (34).

In order to evaluate the stability or robustness of the resulting signatures, a Rand index was also calculated. With k runs (e.g., the resulting gene lists by training on k different datasets) of an algorithm, the Rand index is defined as

where ∩ represents the size of intersection between two gene lists, and ∪ represents the size of union between two gene subsets gsi and gsj, where gsi and gsj were obtained from the ith and jth runs, respectively. Given the present study aims to select subtype-specific prognostic genes for AC and SCC, these metrics were calculated separately for AC and SCC.

The proposed procedure consisted of three steps. Firstly, all 8,023 genes were ranked in the ascending order according to their GeneRanks. Secondly, for a specific k value (k varies from 200 to 7,800 with an increment of 200 to 8,023), the search space (the number of genes under consideration) was restricted to those on the top k of this ordered gene list, and the corresponding adjusted P-values for β2 and (β2+β3) coefficients for a gene and the absolute average of its correlation coefficients with other genes in the search space were considered together to select prognostic genes for AC and SCC. Finally, the sign averages for AC- and SCC-specific genes and the performance statistics were calculated. Steps 2 and 3 were repeated over all possible k values. The optimal k value for AC and SCC subtypes is the one with the largest C-statistics and the smallest sizes of the resulting gene signatures on the training set. Fig. 1 illustrates the proposed procedure, which is referred to as the Cox filter method with redundant gene elimination (RGE) herein.

Figure 1. Flowchart for the proposed Cox filter method with redundant gene elimination. The Cox filter + RGE method may be divided into three steps: i) Ascending ranking of genes under consideration according to the ranks given by the GeneRank method; ii) restricting the search space to the first k genes and fitting the Cox filter models for these k genes; and iii) calculating the corresponding P-values and average absolute Pearson's correlation coefficients for each gene and determining the relevance level of the gene (with P-value<0.01 and corgs<0.2 deemed to indicate relevance). Steps 2 and 3 are repeated over a grid of values for k (k=200, 400, …7800, 8023). AC, adenocarcinoma; HPRD, Human Protein Reference Database; PCC, Pearson's correlation coefficient; RGE, redundant gene elimination; SCC, squamous cell carcinoma.

The proposed procedure first imposed search space restriction and subsequently removed redundant genes inside the restricted search space. One may argue a procedure in the reverse order, i.e., the removal of redundant genes followed by search space restriction, may lead to same or at least similar results. However, conducting redundant gene elimination first may result in the remaining genes being almost uncorrelated with each other. The connectivity weights of those genes are approximately at the same level, and the rearrangement of genes according to GeneRanks becomes meaningless. This method also does not take into consideration pathway information, Alternatively, a strategy instead of a combination of the GeneRank method and redundant gene elimination may be employed. However, this was not investigated as it is beyond the scope of the present study.

Biological relevance and gene set enrichment analysis

The GeneCards database (www.genecards.org) was used to search for the biological relevance of the selected genes, and the String software (www.string-db.org) was used to obtain enriched pathways/gene sets for the AC-specific and SCC-specific prognostic signatures.

Statistical language and packages

R language (version 3.2; www.r-project.org) was used to carry out all statistical analysis in the present study. The R packages used included survival, survAUC, gelnet, pathClass, limma, annotation, affy and hgu133plus2.db.

Results

In the present study, the integrated data of three microarray experiments were used to train the final models. The performance of the resulting prognostic signatures was validated on the RNA-Seq dataset, which is independent from the microarray datasets. Firstly, Schoenfeld residuals were calculated to test the proportional hazards assumption of the Cox models. The P-values for those tests ranged from 0.003 to 0.9999; P<0.05 for 141 values and P<0.01 for 27 values. These numbers were <5% and 1% of the total number of genes. Therefore, the proportional hazard assumption is valid in the present study.

The C-statistics and the model sizes on the training set are given in Fig. 2. Based on these two statistics, the resulting signatures of the first 1,000 genes for AC and the first 4,000 genes for SCC were chosen and presented in Table I. In the same table, the performance statistics for the Cox filter method (15) with search space restriction but without redundant gene elimination, the Cox filter method with redundant gene elimination but no space restriction and the original Cox filter method (corresponding to the Cox filter method without both redundant gene elimination and space restriction) and two other relevant algorithms (the Cox-TGDR method (16) and the LASSO (35) for AC and SCC, respectively) were also listed.

Figure 2. Determination of the optimal cutoffs for AC subtype and SCC subtype search spaces by training of the NSCLC microarray data: (A) The C-statistic under all scenarios (with k taking different values, i.e., k=200, 400, …7800, 8023; (B) The sizes of resulting prognostic signatures under all scenarios. The C-statistic and the final sizes determine the optimal cutoffs for the restricted search space of AC and SCC, respectively, i.e., the one with the largest C-index and the smallest final model size was chosen. AC, adenocarcinoma; NSCLC, non-small cell lung cancer; SCC, squamous cell carcinoma.

Table I. Performance statistics for the non-small cell lung cancer application using different algorithms.

Table I.

Performance statistics for the non-small cell lung cancer application using different algorithms.

			C-statistics
Variable	Size	Rand index (%)	Training set	Test set
G(1)~G(1000) + RGE: AC	35	26.97	0.725	0.694
G(1)~G(4000) +RGE: SCC	44	16.84	0.833	0.817
G(1)~G(1000): AC	45	26.04	0.703	0.714
G(1)~G(4000): SCC	380	26.91	0.702	0.771
Cox-filter +RGE: AC	259	16.67	0.699	0.610
Cox-filter +RGE: SCC	119	15.44	0.824	0.805
Cox-filter: AC	329	24.05	0.681	0.538
Cox-filter: SCC	836	27.85	0.714	0.778
Cox-TGDR: AC	62	7.78	0.684	0.559
Cox-TGDR: SCC	76	5.77	0.721	0.567
LASSO: AC	9	14.87	0.724	0.583
LASSO: SCC	10	12.39	0.814	0.706

[i] G₍₁₎~G_(k): The search space is the first k genes ordered by the GeneRank method. The results were trained using the integrated dataset and verified using the TCGA RNA-sequencing data. AC, Adenocarcinoma; RGE, redundant gene elimination; SCC, squamous cell carcinoma; TGDR, Threshold Gradient Descent Regularization.

The most important finding is that the additional redundant gene elimination indicates significant gains in terms of performance statistics, i.e., better C-statistics and smaller sizes of the resulting signatures, which is in consistent with the findings of other investigators (31,36). Of note, it is usually common that the test set has a poorer performance compared with the training set, due to the following reasons: i) The different characteristics among patients in the training set and the test set; or/and ii) the potential of over-fitting. Given a moderate value of >0.6 for the C-index is regarded to have a satisfactory performance (33), the predictive performances of the resulting prognostic signatures obtained by the proposed procedure are all acceptable. Furthermore, the training set used previously (i.e., the data of GSE50081) has a moderate sample size. To date, a perfect performance has not been achieved with the test set using this specific training set (14–16). To address this, two additional microarray experiments were included, and the training set used in the present study is a combination of all three studies. The resulting signatures trained from the integrated data outperform the signatures from GSE50081.

Another finding is that with a suitable restriction on the search space, the resulting prognostic signatures tend to have a better performance than those without such a restriction (as shown in Table I and Fig. 2). This supports the use of a pre-filtering process (e.g., ranking genes using the GeneRank method on expression levels and importance level in the gene network following by selecting the top genes in the resulting list) prior to downstream analysis. A pre-filtering process may screen out the genes that are highly unlikely to be relevant genes and thus reduces the computing burden. Compared with other relevant algorithms, the Cox filter method has the best performance. The Cox filter method is easier to implement and more computationally efficient than the Cox-TGDR method, which may make the advantage of a pre-filtering procedure with regards to reducing the computing burden less obvious. However, the present authors do not exclude the probability that the Cox-TGDR method is optimal for some specific data structures, and therefore such an advantage is more essential in those applications.

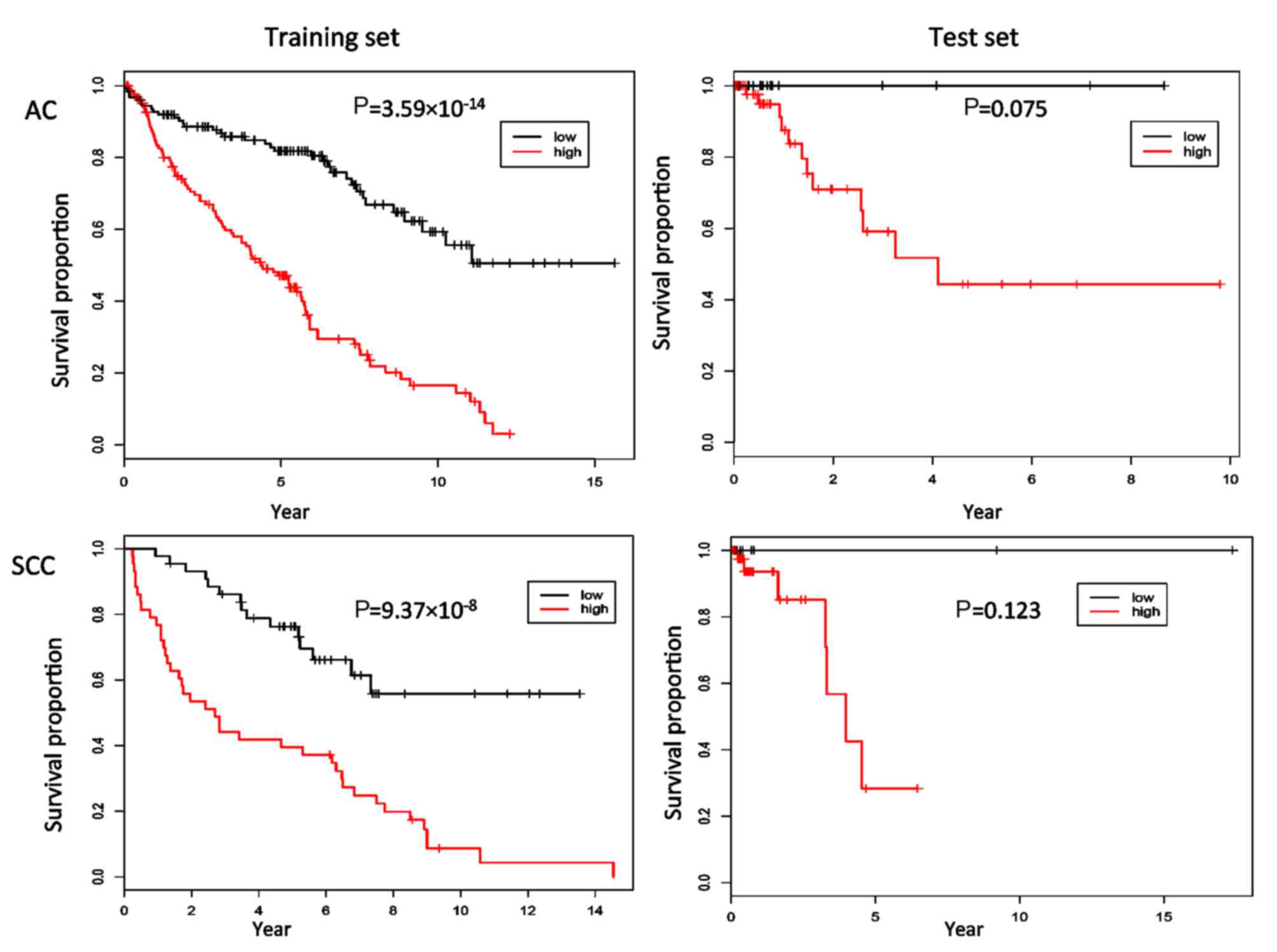
The patients were stratified into two groups-patients with a high risk of mortality and those with a low risk of mortality-by using the median values of the resulting sign average scores for the patients in the training set. Then, the Kaplan-Meier curves were constructed (Fig. 3), and the two curves were compared using log-rank tests. In the training set, the P-values of the corresponding log-rank tests were 3.59×10−14 for AC and 9.37×10−8 for SCC, respectively. However, the corresponding P-values were 0.075 and 0.123 in the test set, indicating a statistically non-significant difference between the survival curves of the high-risk and low-risk groups. Furthermore, other cutoffs (mean, the first and third quartiles) were used, and the results remained the same. Given there were few mortalities recorded for the RNA-seq data and there were no mortalities in the identified low-risk groups, the predictive performance evaluated on the basis of the log-rank tests is still acceptable.

Figure 3. Kaplan-Meier plots of AC-specific prognostic signature and SCC-specific prognostic signature. Based on the risk scores (i.e., the sign averages of AC-specific signature for AC patients and the sign averages of SCC-specific signature for SCC patients), patients were divided into two categories (low-risk group and high-risk group) using the medians of risk scores as cutoffs. The P-values of log-rank tests comparing the survival curves of the low-risk and high-risk groups are shown. AC, adenocarcinoma; SCC, squamous cell carcinoma.

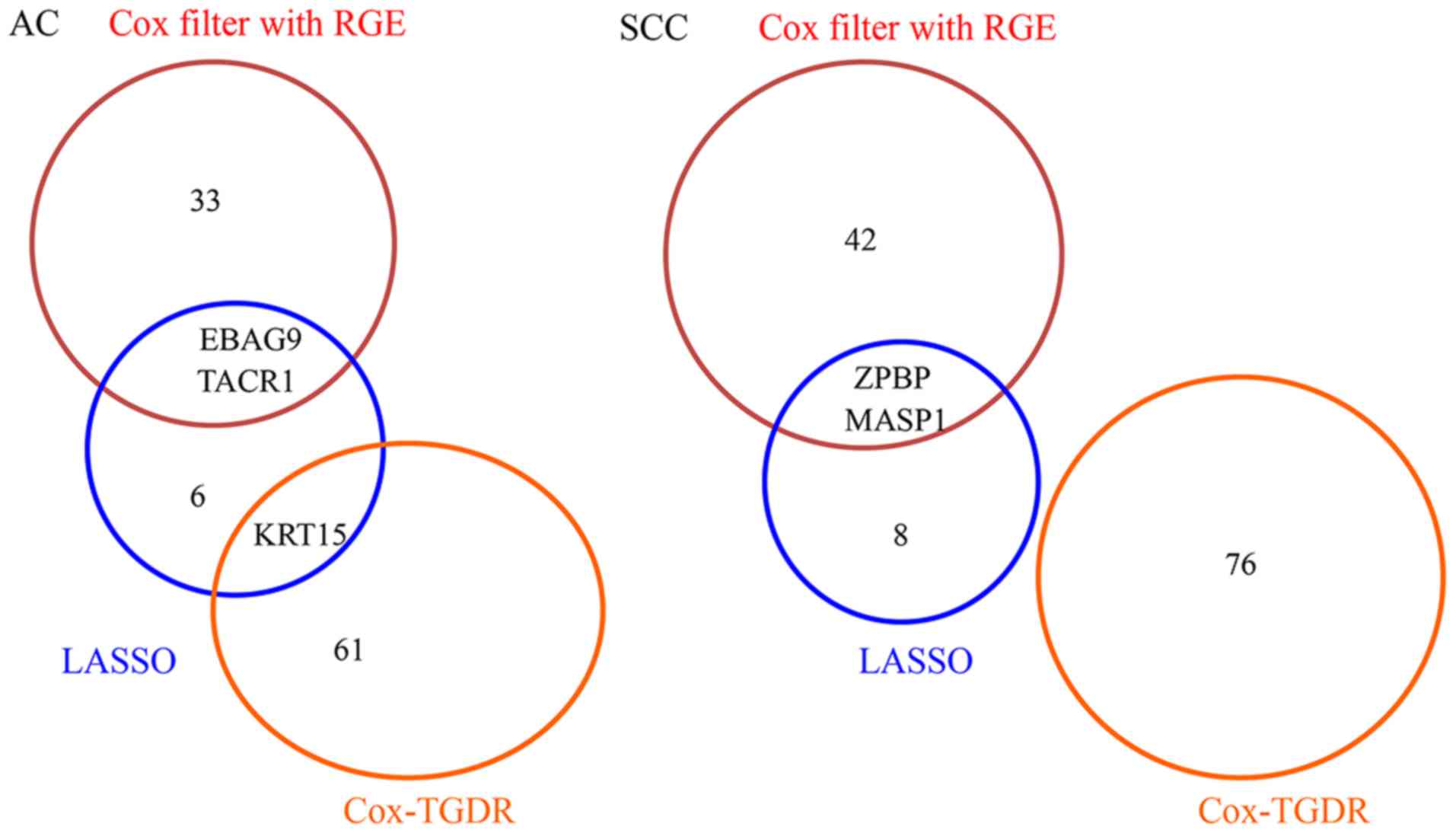
For the 35-gene AC-specific prognostic signature and the 44-gene SCC-specific prognostic signature, the GeneCards database was searched for the biological relevance of these selected genes. According to the GeneCards database, CYP1A2, EGAG9, BRDT, DDC, ADCYAP1R1, PIWIL4, CENT2, TACR1, ABCA2 and NEFH are directly associated with LC. EGAG9, CYP1A2, CRISP3, BRDT, BRSK1, DDC, TACR1, ABCA2, CTNNA3, CCNO, TAC3 and CA6 are directly associated with AC among the AC-specific signatures. Among the SCC-specific signatures, CP19A1, CYP3A4, KLF2, ACLY, MASP1, SOX18, SERPINE2, BHLHE41, PDYN, FGF4, NUAK1, GCNT1, CCT4 and EBNA1BP2 are directly associated with LC. FGF4, CYP19A1, PTPN2, CYP3A4, SERPINE2, SOX18, MMP20, MASP1, KLF2, ERP44, NUAK1 and RAET1E are directly associated with SCC. All respective remaining genes in each category were indirectly associated with LC, AC and SCC. Among the indirectly related genes, many genes were associated with the corresponding diseases through their association with the well-known cancer gene: TP53. Additionally, there was no overlap between the AC-specific and SCC-specific prognostic signatures. Likewise, there was no overlap between the AC-specific prognostic and SCC-specific prognostic signatures when the LASSO method implemented separately for each subtype. By contrast, there were substantial overlaps (32/106, 30.19%) between the AC-specific prognostic signature and the SCC-specific prognostic signature when the Cox-TGDR method was used. The resulting prognostic signatures by the proposed procedure, the Cox-TGDR and the separate LASSO analysis are listed in Table II. The overlapping signatures as identified by the LASSO method, the Cox-TGDR method and the proposed procedure for AC and SCC are presented in Fig. 4.

Figure 4. Venn-diagrams of the respective AC-specific and SCC-specific prognostic signatures as selected by the proposed method, the Cox-TGDR method and the LASSO method. These two Venn-diagrams showed there were no or few overlaps between the signatures selected by different feature selection methods. AC, lung adenocarcinoma; EBAG9, estrogen receptor binding site associated, antigen, 9; KRT15, keratin 15; MASP1, mannan binding lectin serine peptidase 1; RGE, redundant gene elimination; SCC, lung squamous cell carcinoma; TACR1, tachykinin receptor 1; TGDR, Threshold Gradient Descent Regularization; ZBP1, Z-DNA binding protein 1.

Table II. Resulting prognostic gene signatures by the proposed procedure, the Cox-TGDR method and the separate LASSO analysis for each subtype.

Table II.

Resulting prognostic gene signatures by the proposed procedure, the Cox-TGDR method and the separate LASSO analysis for each subtype.

Cox filter with RGE		LASSO		Cox-TGDR
AC-specific (44.3%)	SCC-specific (55.7%)	AC-specific (47.4%)	SCC-specific (52.6%)	AC-specific (28.3%)	SCC-specific (41.5%)	Overlapped genesa (30.2%)
N4BP3	PASK	EBAG9	ZPBP	ELSPBP1	N4BP3	COMMD6
NLRP4	EIF1AY	KRT15	TENC1	AKAP4	GNRHR	DR1
ADCYAP1R1	SLC22A9	TACR1	RAD50	RHOD	PAH	MICALCL
GRM6	ZNF518A	FCER1A	CRYAA	CD177	MBD6	PRMT6
ERMAP	CYP3A4	C6orf203	MASP1	ALOX12B	VAV2	SEMA3A
GRK7	PLAC8	WNT7A	IL1A	MMP3	APIP	IBTK
TACR1	EBNA1BP2	ENG	SATB1	ACTR1B	RDX	HUS1B
CTNNA3	NYNRIN	LMTK2	CDH5	ABCC2	CLNK	DDB2
PAH	BHLHE41	NF2	TMF1	TTPAL	SLC1A6	RNF32
CCNO	EVC2		AKT1	DNAJB2	STXBP6	PPCDC
RAB3C	NCOA7			SLC6A2	HIST1H1C	ZNF91
CA6	NUAK1			PKP1	LMX1A	DRD4
SPINK5	CPN2			GCNT1	GPR26	IL5RA
PIWIL4	CYP19A1			STRA13	RAPSN	ASCL2
RABGAP1	BCAP29			NUMA1	PSMF1	GABARAPL1
SLC22A4	KCNJ8			IL1F10	EPHA4	NRG1
NEURL2	FAM115A			E2F2	UPK2	GTF2A1L
SNX24	CKAP2			SLC2A4	RGS13	PRLHR
BRDT	KLF2			RNF220	NUP88	DCP1B
NEFH	SOX18			AP4E1	RRP1B	NUP205
PLCD4	ANKRD7			LSM10	FUBP3	PLEKHG4
ABCA2	PKN2			CPSF7	NFIB	EMB
DDC	FGF4			TRIM63	KRT85	ADAM2
CRISP3	PTPN2			ALOX12	RAD52	SSR4
SIRPB1	GCNT1			CEACAM3	PRKAG1	FAM71C
CWC25	GABRA4			CARD16	CD3EAP	KRT2
AAGAB	TAF1B			COL23A1	ARG1	SIM1
SAP30L	CCT4			SARS2	KCNA10	PAPPA2
FBXO44	CCDC42			PITX1	FGF10	EPB41L1
EBAG9	BFSP2			NGFR	ZNF417	PAIP2B
BRSK1	ZFAND5				MAP4	TM4SF1
GABRB1	SERPINE2				ATG4B	KRT15
CYP1A2	RBM11				FANCC
CETN2	PDYN				JDP2
TAC3	PGS1				EIF2B1
	RAET1E				KLK6
	RYR3				LINGO1
	ZPBP				RFXAP
	SLC17A1				ZBTB25
	ACLY				IL5
	MMP20				S100A1
	NUDT5				BIRC3
	ERP44				GRIN2B
	MASP1				FBXW7

a Genes that are overlapped between the AC-specific prognostic signatures and the SCC-specific prognostic signatures. The proportion of each stratum (i.e., AC-specific genes, SCC-specific genes and overlapped genes) was listed below each category. AC, lung adenocarcinoma; SCC, lung squamous cell carcinoma; RGE, redundant gene elimination; TGDR, Threshold Gradient Descent Regularization.

Given there was no overlap between the AC-specific and SCC-specific prognostic signatures, how these signatures intersected at the pathway level was examined. Using the String software, enriched pathways/gene sets for the AC-specific prognostic SCC-specific prognostic signatures were searched separately. Using the default cutoff value of 0.05 for the False Discovery Rate (FDR), there were 5 GO Biological Process (BP) terms, 1 GO Molecular Function (MF) terms, 4 GO Cellular Component (CC) terms and 0 KEGG pathways that were significantly enriched by the AC-specific prognostic genes, respectively. These sets of gene are listed in Table III. By contrast, there were 11 BP terms, 0 MF terms, 23 CC terms and 2 KEGG pathways that were significantly enriched for the SCC-specific genes. The enriched gene sets for the SCC-specific prognostic signature are listed in Table IV. Furthermore, there was no overlap between the enriched gene sets for AC and SCC, indicating the pathways enriched by the subtype-specific genes differ. With redundant gene elimination, the identified AC-specific and SCC-specific signatures differ completely at the levels of genes and pathways. By contrast, without redundant gene elimination, there were substantial overlaps between the identified signatures, which suggest redundant gene elimination is beneficial for identifying those genes that are specific for a particular subtype.

Table III. Enriched GO terms and Kyoto Encyclopedia of Genes and Genomes pathways using the 35-gene lung adenocarcinoma-specific prognostic signature.

Table III.

Enriched GO terms and Kyoto Encyclopedia of Genes and Genomes pathways using the 35-gene lung adenocarcinoma-specific prognostic signature.

Pathway ID	Pathway description	FDR
Cellular component
GO.0002199	Zona pellucida receptor complex	4.84×10−14
GO.0005832	Chaperonin-containing T-complex	8.25×10−12
GO.0044297	Cell body	3.66×10−4
GO.0005874	Microtubule	5.04×10−3
Biological process
GO.0007339	Binding of sperm to zona pellucida	1.39×10−8
GO.1901998	Toxin transport	1.50×10−6
GO.0051084	De novo posttranslational protein folding	3.32×10−6
GO.0007338	Single fertilization	6.64×10−6
GO.0006457	Protein folding	5.19×10−4
Molecular function
GO.0051082	Unfolded protein binding	2.37×10−3

[i] The 35-gene lung adenocarcinoma prognostic signature was identified using the Cox filter method with redundant gene elimination. The search space was restricted to the first 1,000 genes (the orders were obtained using the GeneRanks method). FDR, False Discovery Rate; GO, Gene Ontology.

Table IV. Enriched GO terms and KEGG pathways using the 44-gene SCC subtype specific prognostic signature.

Table IV.

Enriched GO terms and KEGG pathways using the 44-gene SCC subtype specific prognostic signature.

Pathway ID	Pathway description	FDR
Cellular component
GO.0005681	Spliceosomal complex	1.12×10−13
GO.0071013	Catalytic step 2 spliceosome	5.34×10−12
GO.0030529	Ribonucleoprotein complex	2.33×10−7
GO.0071942	XPC complex	7.11×10−6
GO.0097525	Spliceosomal snRNP complex	9.11×10−6
GO.0005686	U2 snRNP	2.25×10−4
GO.0016607	Nuclear speck	1.37×10−3
GO.0005654	Nucleoplasm	4.32×10−3
GO.0044428	Nuclear part	4.32×10−3
GO.0000974	Prp19 complex	5.58×10−3
GO.0005684	U2-type spliceosomal complex	1.66×10−2
GO.0043227	Membrane-bounded organelle	1.68×10−2
GO.0032991	Macromolecular complex	1.76×10−2
GO.0043226	Organelle	1.76×10−2
GO.0044424	Intracellular part	1.76×10−2
GO.0031981	Nuclear lumen	2.31×10−2
GO.0097458	Neuron part	2.40×10−2
GO.0031410	Cytoplasmic vesicle	2.49×10−2
GO.0044446	Intracellular organelle part	2.49×10−2
GO.0005622	Intracellular	3.01×10−2
GO.0016023	Cytoplasmic membrane-bounded vesicle	4.67×10−2
GO.0036477	Somatodendritic compartment	4.67×10−2
GO.0043231	Intracellular membrane-bounded organelle	4.67×10−2
Biological process
GO.0000398	mRNA splicing, via spliceosome	3.62×10−11
GO.0008380	RNA splicing	2.74×10−10
GO.0006397	mRNA processing	2.33×10−9
GO.0007217	Tachykinin receptor signaling pathway	2.60×10−9
GO.0060359	Response to ammonium ion	4.28×10−3
GO.0000715	Nucleotide-excision repair, DNA damage recognition	9.43×10−3
GO.0043279	Response to alkaloid	1.64×10−2
GO.0032355	Response to estradiol	2.00×10−2
GO.0043278	Response to morphine	4.27×10−2
GO.0046878	Positive regulation of saliva secretion	4.27×10−2
GO.0006289	Nucleotide-excision repair	4.38×10−2
KEGG pathways
3040	Spliceosome	4.66×10−19
3420	Nucleotide excision repair	3.49×10−2

[i] The 44-gene SCC prognostic signature was identified using the Cox filter method with redundant gene elimination. The search space was restricted to the first 4,000 genes (The orders were obtained using the GeneRanks method). FDR, False Discovery Rate; GO, Gene Ontology; KEGG, Kyoto Encyclopedia of Genes and Genomes; SCC, squamous cell carcinoma.

Discussion

In this article, the Cox filter model was extended to solve two additional issues. One issue was how to incorporate pathway information by excluding the genes with less importance in the gene-to-gene interaction network. The other issue involved eliminating the potential redundant genes by adding an extra restriction on the average absolute correlation coefficients of a gene with other genes in the search space.

Using NSCLC gene expression data, it was demonstrated that the proposed method does outperform the original Cox-filter method and the Cox-TGDR method. Similar to the Cox filter method, the Cox-TGDR method is capable of identifying subtype-specific prognostic genes and does not take pathway information into consideration. However, it is superior to the original Cox-filter method in terms of redundant gene elimination, since it considers the additive effects among genes, so the proposed method presents certain advantages.

Apart from different objectives, there are substantial differences between the present study and a previous study by the authors (14). Firstly, the patients were classified into either the high-risk group or the low-risk group according to survival time in the previous study (14). Secondly, no separation on AC and SCC subtypes was made in the previous study (14), therefore the resulting signatures were general for these two subtypes instead of being specific for each subtype. Thirdly, the Radical Coordinate Visualization plot (36), which was used for feature selection in the previous study (14), imposes restrictions on the maximal size of a resulting gene signature. Finally, GSE50081, which was used as the training set in the previous study (14), accounted for 40% of the size of the integrated data. In the previous study, it was concluded that no good separation between the two risk groups was obtained; since the best C-index (the same test set was used in these two studies) was only 0.54 (14). By contrast, the present study used survival time data directly and a larger data set to identify subtype-specific prognostic genes with the Cox filter method, which has no restriction on the maximal size of a signature. With these advantages, the C-statistics have been improved dramatically in the present study.

Consistent with other studies (31,37), it was demonstrated in the present study that redundant gene elimination has beneficial effects on feature selection. With redundant gene elimination by comparing the Cox filter method with RGE and the original Cox filter method, the resulting signatures have better predictive performance, smaller model sizes and more subtype-specific genes. Furthermore, the present study demonstrated that the use of a pre-filtering process prior to downstream analysis is very beneficial, which is consistent with previous findings by the authors (9) and the work by others (38,39). Therefore, it is highly recommended to carry out the pre-filtering process, particularly when a very complicated and time-consuming statistical method was selected for downstream analysis. Certainly, the method of conducting the pre-filtering procedure is also of importance. In the present study, the GeneRank method was used, which considers pathway information. Numerous studies have previously demonstrated that incorporating pathway information improves the predictive capacity of a feature selection method (21–25). Likewise, a pre-filtering procedure that incorporates pathway information is also more helpful for a feature selection process. To conclude, the GeneRank method is preferable as a pre-filtering procedure over a method that does not consider any pathway information, such as moderated t-tests in the R limma package (30).

Acknowledgements

The author would like to thank Ms. Bing Wang of Jilin University for preparing the TIFF formatted figures.

Funding

The present study was supported by the Natural Science Foundation of China (grant no. 31401123).

Availability of data and materials

All data used in present study were publicly assessable. Specifically, the microarray data included GSE30219, GSE37745 and GSE50081 datasets from the Gene Expression Omnibus (GEO, https://www.ncbi.nlm.nih.gov/geo/) repository, and the RNA-Seq data were downloaded from The Cancer Genome Atlas Data Portal (level 3) (https://tcga-data.nci.nih.gov/tcga/).

Authors' contributions

ST conceived and designed the study, analyzed the data and interpreted the results and wrote the paper.

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.

References