This article is mentioned in:

Introduction

Ankylosing spondylitis (AS) is an immune-mediated arthritis and is the prototypic member of a group of conditions known as spondyloarthropathies, which also includes reactive arthritis, psoriatic arthritis and enteropathic arthritis (1). Several features, such as synovitis, chondroid metaplasia, cartilage destruction and subchondral bone marrow changes, are commonly observed in the joints of patients with AS (2). Due to the complex progression of the joint remodeling process, clinical research has not systematically evaluated histopathological changes (3), and no clear sequence of the pathological mechanism has been obtained for this disease.

With the development of high throughput technology and gene data analysis over the past decade, rapid progress has been made in the discovery of genetic associations with AS, which has provided novel insights on the aetiopathogenesis of the disease (4). It had been demonstrated that ~90% of patients with AS expressed the human leukocyte antigen-B27 genotype (5). A study by Lin et al (6) investigated the pathophysiological significance of interleukin-27 and vascular endothelial growth factor in AS. In addition, the Wnt pathway was revealed to have a critical contributing role in the unique pathology and bony fusion in AS (7). However, these studies did not identify an effective clinical target therapy or the underlying molecular mechanism of AS.

Therefore, the aim of the present study was to identify differential modules between AS and healthy controls by integrating network analysis, module inference and the attract method, and provide insights on the pathological mechanism and future studies of AS. Here, network analysis may provide significant instructions for mining unknown connections in incomplete networks. Although the data of large-scale protein interactions continue to accumulate, a certain number of significant interactions are not tested (8). This type of difficulty may be resolved to some extent by utilizing sub-network or module inferences of the complex network (9). Meanwhile, attract is a knowledge-driven analytical approach for identifying and annotating the gene sets that best discriminate between cell phenotypes (10), and thus the present study utilized this to identify differential modules between the AS and healthy groups.

Materials and methods

Identification of differential modules between AS patients and healthy controls

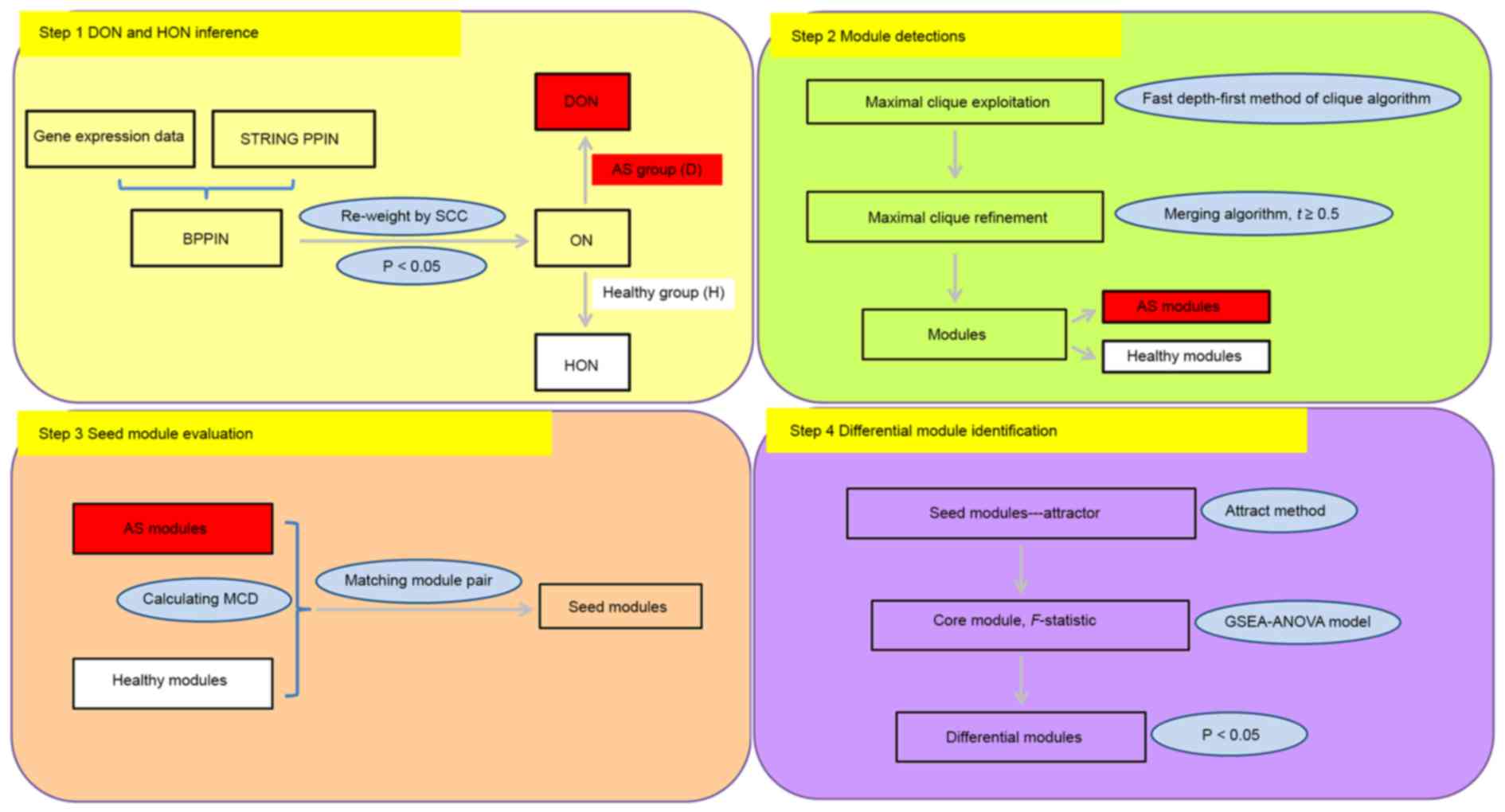
The identification of differential modules between AS patients and healthy controls comprised four steps (Fig. 1): Disease objective network (DON) and healthy objective network (HON) inference dependent on gene expression data using the Search Tool for the Retrieval of Interacting Genes/Proteins (STRING, https://string-db.org/), the protein-protein interaction network (PPIN) and Spearman's correlation coefficient (SCC); module detection by using the clique-merging algorithm; seed module evaluation through module correlation density (MCD) calculation and module pair match; and differential module identification based on the attract method.

Figure 1. Flow chart of differential module inference. DON, disease objective network; HON, healthy objective network; STRING, Search Tool for the Retrieval of Interacting Genes/Proteins; PPIN, protein-protein interaction network; BPPIN, background protein-protein interaction network; SCC, Spearman's correlation coefficient; AS, ankylosing spondylitis; MCD, module correlation density; GSEA-ANOVA, gene set enrichment analysis-analysis of variance.

DON and HON inference

Gene expression data

Gene expression data of E-GEOD-25101 for AS patients and healthy controls was recruited from the ArrayExpress database (https://www.ebi.ac.uk/arrayexpress/). E-GEOD-25101 consisted of 16 AS samples and 16 healthy samples in total, and was presented on an A-MEXP-1171-Illumina HumanHT-12 v. 3.0 Expression BeadChip Platform (Illumina, Inc., San Diego, CA, USA). Subsequently, the following standard procedures were conducted to control the quality of the data: Background correction based on the Robust Multi-array Average (RMA) algorithm (11); normalization according to the quantile based algorithm (12); probe correction by the Micro Array Suite (MAS) algorithm (13); and expression summarization using the median polish method (11). By converting the preprocessed data on probe level into gene symbol measures, a total of 11,587 genes were obtained in the gene expression data for further exploitation.

Background protein-protein interaction network (BPPIN) extraction

A dataset of literature-curated human PPIN from the STRING database was utilized, comprising 16,730 genes and 1,048,576 interactions (14). Genes or interactions without an expression value or duplicated self-loops were removed. The remaining largest connected component with a score >0.8 was kept as the global PPIN, which was composed of 5,665 nodes and 28,176 edges. To make the global PPIN more confident and reliable, intersections between the global PPIN and gene expression data were taken, and the intersected network was termed BPPIN.

DON and HON construction

For the purpose of re-weighting gene interactions in the BPPIN of the AS and healthy conditions, SCC was implemented (15). SCC is a measure of the correlation between two variables, giving a value between −1 and +1, inclusive. The SCC (x, y) was calculated using the following formula:

Where n was the number of samples of the gene expression data; g (x, i) or g (y, i) was the expression level of gene x or y in the sample i under a specific condition; and g(x) or g(y) represented the mean expression level of gene x or y.

If SCC (x, y) had a positive value, there was a positive linear correlation between x and y. For an interaction between gene x and y, the absolute SCC value was denoted as its weight value. Only the interactions with P<0.05 were selected to construct the objective network. DON was for disease (AS group) and HON was for the healthy group.

Module detection

Identifying modules from DON and HON for the disease and healthy groups was conducted using the clique-merging algorithm (16,17). This process predominantly included two steps: Exploring maximal cliques using the clique algorithm and refining or merging maximal cliques with high overlap.

Maximal clique exploration

The cliques algorithm proposed by Tomita et al (18) was applied to search maximal cliques. It utilized a depth-first search strategy to enumerate all maximal cliques and effectively removed non-maximal cliques during the enumeration process. The score of a clique, C, was defined as its weighted interaction density (WID):

Where w (x, y) represented the weight of the interaction between gene x and y. Due to cliques with a too small or large number of genes was difficult and meaningless to study; therefore, cliques with node amount <4 were discarded (19). Furthermore, maximal cliques were obtained by ranking the cliques on the basis of WID in descending order.

Maximal clique refinement

Various maximal cliques may overlap with one another as thousands of them were generated from a DON or HON. The highly overlapped maximal cliques must be merged to reduce the result size. For every clique Ci, it was checked whether another clique Cj existed such that Cj had a lower score than Ci and |Ci∩Cj|/|Cj| ≥t, where t=0.5 was a predefined threshold for overlapping (20). If such Cj existed, the inter-connectivity scores between Ci and Cj were used to decide whether to remove Cj or merge Cj with Ci. The refined maximal cliques were denoted as modules. Notably, modules were identified based on DON and HON for the disease group and healthy group, respectively.

Seed module evaluation

In the present study, AS and healthy modules were matched, which ensured that the module pairs had the same or similar gene composition but different interactions. The Jaccard index (21), which is the ratio of intersection over union for two sets, was applied to evaluate the matching degree. The modules with Jaccard score ≥0.5 were considered to be seed modules.

Meanwhile, the set of disease modules was expressed as Di, and Hj was used for the healthy module set. In order to further evaluate the relationships among seed modules, MCD was utilized. For disease module set Di, MCD was computed according to following equation:

Of which M was a similarity graph to perform a maximum weight bipartite matching (22). MCD of healthy modules, MCD(Hj), was calculated similarly. The modules were ranked in non-increasing order of their absolute differential density, ∆C = |MCD(Dj)-MCD(Hj)|.

Differential module identification using the attract method

To identify altered modules between AS patients and healthy controls more accurately than seed modules, differential modules were identified utilizing the attract method, which is a knowledge-driven analytical approach for identifying and annotating gene sets (10). The method may be summarized in four steps (23): Determining core modules that discriminated most strongly between cell types or experimental groups of interest; finding different synexpression groups that were present within a core attractor module; identifying sets of genes that demonstrated highly similar profiles to the synexpression groups within an attractor module; and testing for functional enrichment for each of the synexpression groups to detect any potentially shared modules.

In the present study, each seed module was regarded to an attractor. Based on the attract method, a gene set enrichment analysis-analysis of variance (GSEA-ANOVA) model was utilized to assess module level data and investigate differential modules between the AS group and healthy group. The core module was identified through the F-statistic, for gene x, F(x) was computed as follows:

Where v represented the corresponding expression value in each replicate sample; rk represented each cell type k = 1, …, K; u represented the mixed effect model; and N represented the total number of samples. Large values of the F-statistic indicated a strong association, whereas a small F-statistic suggested that the gene demonstrated minimal cell type-specific expression changes. To make the F-statistic more reliable, t-tests were used to correct the log2-transformed F-statistics and obtain P-values for each potentially shared module that originated from synexpression groups. By adjusting their P-values on the basis of false discovery rate (24), the modules with P<0.05 were defined as differential modules between AS and controls.

Results

DON and HON

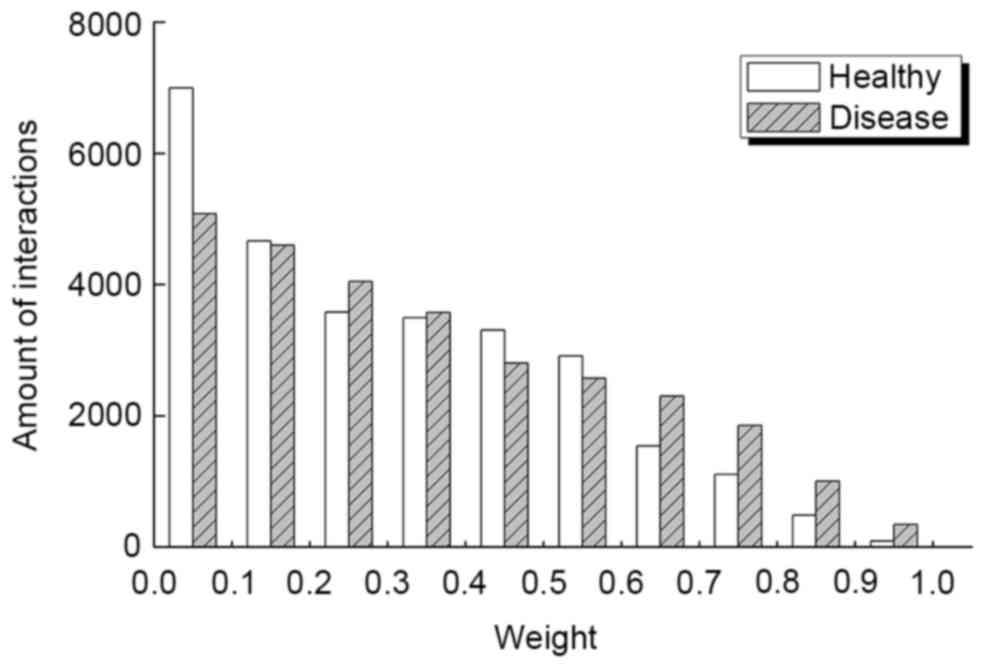
By integrating gene expression data, STRING PPIN and SCC-related analysis, the DON and HON that displayed an equal number of nodes (5,301) and interactions (28,176) for the disease group and healthy group were identified. However, the weight distributions for the two networks were different, as demonstrated in Fig. 2. Results indicated that there were marked differences between the healthy and disease groups in the section of 0–0.1 and 0.6–1.0. When examining these interactions more carefully, the average weight for DON and HON was 0.332 and 0.317, respectively.

Figure 2. Weight distribution of interactions in disease objective network and healthy objective network, according to Spearman's correlation coefficient.

Module detections

In the present study, a clique-merging algorithm was implemented to identify modules from DON and HON separately. A total of 4,601 and 4,841 maximal cliques were detected for the disease group and healthy group, respectively, based on the fast depth-first method of the clique algorithm. With the thresholds of node amount> 4, 677 disease maximal cliques and 910 healthy maximal cliques were obtained. Subsequently, these cliques were refined by merging algorithm with t≥0.5 to form modules. A total of 21 modules were gained for the disease group, while 20 modules were identified for the healthy group. The compositions for modules were demonstrated in Tables I (disease group) and II (healthy group).

Table I. Module properties of disease group.

Table I.

Module properties of disease group.

Module	Count	Genes
1	9	RPL35, RPS13, EEF1B2, RPS5, RPL6, RPL18A, RPL19, RPL27, RPLP0
2	12	RPL35, RPS13, RPS20, RPL6, RPS5, RPS19, RPL18A, RPS16, RPL27, RPL36, EIF3K, RPS6
3	5	RPL35, RSL24D1, EEF1B2, EIF3E, RPL30
4	8	PSMA4, PSMA2, PSMA3, PSMA6, PSMD5, PSMD10, RBX1, PSME3
5	5	NDUFAB1, NDUFAB3, NDUFB2, NDUFB5, NDUFA4
6	8	RPL35, RPS13, SRP54, SEC61B, RPL36, RPN2, RPS19, RPL23
7	5	SF3A1, FUS, SRSF9, SRSF1, SNRPG
8	5	PSMA2, SHFM1, PSMA6, PSMB1, PSMD1
9	8	RPL35, RPS13, TRAM1, SEC61B, SPCS1, RPL36, RPL27, SRPR
10	6	PSMD10, PSMA2, PSMD11, PSMA6, SEC61B, PSMD1
11	8	PSMA4, PSMA2, PSMA3, PSMC4, PSMD5, PSMB1, SEC61B, UBC
12	8	EIF3D, RPL18A, EIF3G, EIF3E, EIF3K, RPL36, RPS19, RPL5
13	5	SNRNP70, SF3B6, FUS, SUGP1, SRSF4
14	6	PSMA3, PSMA2, PSMA6, CCND1, CDKN1B, PSMD1
15	5	AURKA, NUSAP1, NCAPG, GINS2, CCNB2
16	5	RBX1, SKP1, SARS2, FBXO44, FBXL3
17	6	PSMD8, PSMD10, PSMA2, PSMC3, CDKN1B, SKP1
18	5	POLR2I, SF3B6, FUS, SRSF1, YBX1
19	6	EIF3D, RPL18A, EIF3G, RPL18, EIF4B, RPS3
20	5	ARHGAP4, RHOQ, RAC2, ARAP3, ARHGEF2
21	5	CEBPZ, WDR12, NIP7, RSL24D1, BRIX1

Table II. Module properties of healthy group.

Table II.

Module properties of healthy group.

Module	Count	Genes
1	5	RPL35, RSL24D1, EIF3E, EEF1B2, RPL11
2	5	CEBPZ, WDR12, NIP7, RSL24D1, BRIX1
3	8	RPL35, RPL6, EEF1B2, RPS13, RPS5, RPL18A, EIF3E, RPL4
4	7	PSMA4, PSMA6, PSMB1, PSMA2, PSMB7, RBX1, ANAPC10
5	6	RPL35, RPL6, RPL8, EIF3D, EIF3E, RPL31
6	10	RPL35, RPL6, RPL8, RPS16, RPL18A, RPS5, EIF3K, EIF3E, RPL18, RPL12
7	6	PSMD10, PSMA2, PSMA6, PSMB1, SHFM1, PSMC6
8	5	NDUFAB1, NDUFB2, NDUFB5, NDUFB3, NDUFA4
9	7	RPL35, RPL6, RPL8, RPL39, RPS13, RPL27, RPS20
10	6	RPL19, RPS16, RPS5, RPL18A, RPL36, RPS6
11	6	PSMD10, PSMA2, CDKN1B, SKP1, PSMD11, PSMC6
12	6	AAAS, NUP37, NUP107, NUPL2, SRSF1, UPF3B
13	5	SSR1, RPS20, TRAM1, RPL27, RPL9
14	6	RPL35, RPL6, TRAM1, RPS20, SEC61B, RPL4
15	8	PSMA4, PSMA6, PSMB1, PSMA2, PSMD10, PSMA3, SEC61B, PSMC2
16	8	RPL35, RPS14, RPS5, RPS16, RPL8, RPS13, RPS20, RPL36
17	5	RPS19, RPL18A, RPL19, RPS12, RPS11
18	5	RPS19, RPL18A, RPL19, RPS12, RPS11
19	6	RBX1, PSMD3, PSMB1, PSMD10, PSMA2, SKP1
20	5	SF3B6, SRSF1, SNRPB2, SUGP1, SNRNP200

Seed module evaluation

A seed module was defined as the modules between two groups with a Jaccard score ≥0.5. Based on this, six seed modules were obtained (Table III). To further explore the correlations of the seed modules across the AS and normal groups, MCD and differential density ΔC was computed. Seed module 1 had the highest ΔC of 0.077 and Jaccard score of 1.000, followed by seed module 2 (ΔC=0.056; Jaccard score=0.667), seed module 3 (ΔC=0.024; Jaccard score=0.500), seed module 4 (ΔC=0.017; Jaccard score=0.572), seed module 5 (ΔC=0.016; Jaccard score=0.545) and seed module 3 (ΔC=0.007; Jaccard score=1.000). Seed module 1 was composed of six genes, including CEBPZ, WDR12, NIP7, RSL24D1 and BRIX1, and seed module 6 included NDUFAB1, NDUFAB3, NDUFB2, NDUFB5 and NDUFA4.

Table III. Properties of seed modules.

Table III.

Properties of seed modules.

	Module			MCD
Seed module	Disease	Healthy	Jaccard score	Healthy	Disease	∆C
1	21	2	1.000	0.402	0.325	0.077
2	3	1	0.667	0.449	0.393	0.056
3	17	11	0.500	0.368	0.345	0.024
4	8	7	0.572	0.386	0.369	0.017
5	1	3	0.545	0.400	0.416	0.016
6	5	8	1.000	0.382	0.375	0.007

[i] MCD, module correlation density; ∆C, differential module correlation density.

Differential modules

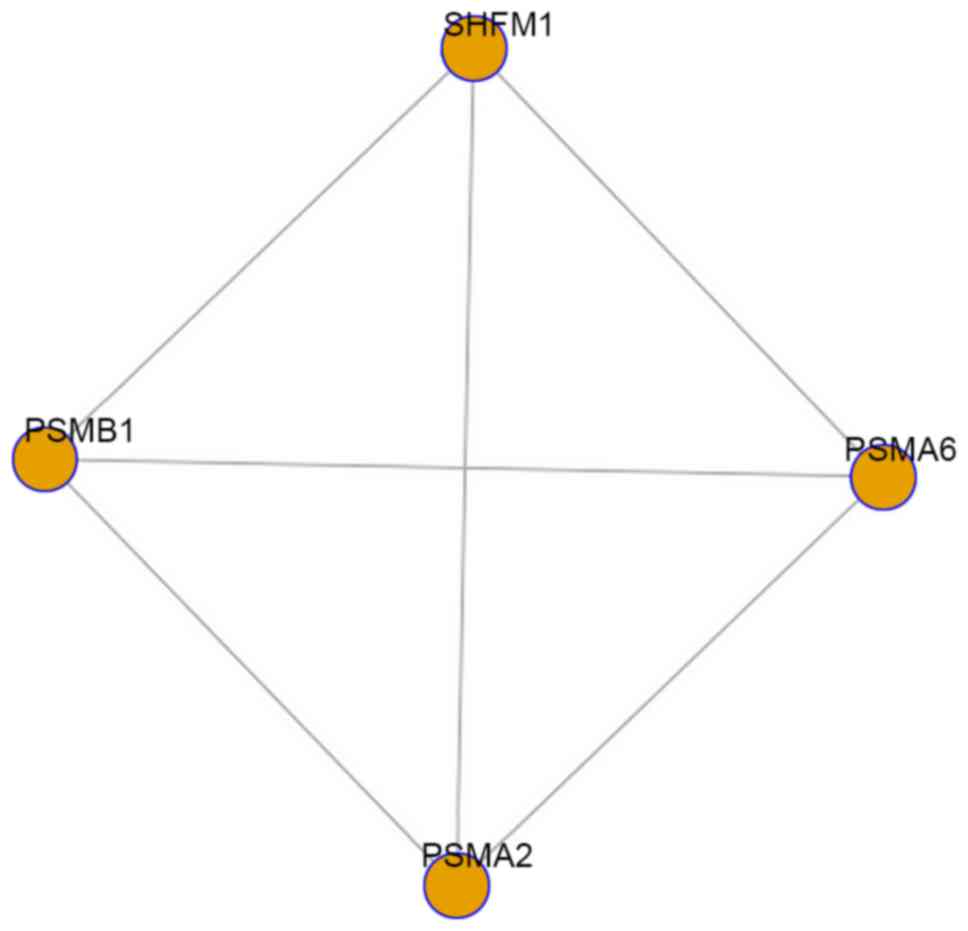
To further investigate significant modules based on seed modules for AS, a GSEA-ANOVA model in the attract method was employed, which also provided a way to gauge which genes were informative for a particular set of cell types. Unlike other GSEA implementations that only allow for two-class comparisons, this ANOVA-based approach tests for differences between multiple classes (24). Supposing that each seed module was an attractor, the differential modules were identified by combining the core module identified through the F-statistic and P<0.05, of which the F-statistic captured the strength of the association observed in a gene's expression over the different groups and P evaluated the significant difference across the two groups. In the present study, a total of one differential module (P=0.015) was obtained between the AS and healthy groups, which was composed of four nodes (PSMA2, SHFM1, PSMA6 and PSMB1) and six edges (Fig. 3). The differential module and its composite genes may have a more significant role than the other modules and genes in the progression of AS and be potential biomarkers for targeted treatment for patients with AS.

Figure 3. Network for the differential modules. Nodes represent genes and edges represent the interactions among any two genes.

Discussion

In the present study, firstly, the DON and HON from the BPPIN of the AS and healthy conditions based on gene expression data, STRING PPIN and SCC, respectively, were extracted. There were 5,301 nodes and 28,176 interactions both in DON and HON; however, the weight distribution of the two networks was different. Secondly, disease and healthy modules were detected from the DON and HON utilizing a clique-merging algorithm. A total of 20 and 21 modules were detected for the AS group and healthy group separately, respectively. Thirdly, seed modules were identified on the basis of a Jaccard score ≥0.5, and six seed modules were obtained. The seed modules were ranked in descending order of ΔC, and seed module 1 had the highest ΔC of 0.077 and Jaccard score of 1.000. Finally, taking each seed module as an attractor, differential modules were identified using a GSEA-ANOVA model in the attract method. A total of one differential module with P=0.015 was obtained between the AS and healthy group.

Traditionally, studies tend to regard differentially expressed genes (DEGs) between normal and disease samples as biomarkers and pathogenic genes; however, DEGs alone may lead to false positives while identifying key genes involved in a disease, as some genes are not involved in the pathway or module of pathogenic genes even though they demonstrate notable expression alterations (25). Studies have indicated that the most significant genes and modules obtained from different studies for a particular disease are typically inconsistent (26). To overcome this problem, one may evaluate pathogenic genes or modules for disease association using a network strategy (27). Therefore, in the present study, modules from DON and HON were identified, which made the results more stable and reliable. Following this, differential modules between the AS condition and healthy controls were identified, which provided potential target biomarkers for patients suffering from AS.

The differential module was composed of four nodes (PSMA2, SHFM1, PSMA6 and PSMB1) and six edges, of which PSMA2, PSMA6 and PSMB1 belonged to the proteasome subunit family. Proteasomes are protein complexes in eukaryotic cells and cleave peptides in an adenosine 5′-triphosphate-/ubiquitin-dependent process in a non-lysosomal pathway, some of which are involved in presentation by major histocompatibility complex class I molecules (28). Upregulation of proteins involved in inflammation and the ubiquitin proteasome pathway have been identified in AS (29), and may have an important role for B27 positive individuals in the development of AS (30). It had been demonstrated that proteasome inhibition aggravated tumor necrosis factor-mediated bone resorption (31). Furthermore, a study by Zhao et al (32) reported that PSMA6 had the potential to be a biomarker for AS by utilizing bioinformatics approaches. Therefore, in the present study, the proteasome family was closely associated with AS, and it is possible to infer that the differential module had a notable role in the progression of AS.

In conclusion, the present study identified one differential module with four nodes (PSMA2, SHFM1, PSMA6 and PSMB1) between AS patients and healthy controls. The present findings may provide insight on the underlying pathological mechanism of AS. Further study should focus on the validation of these mechanisms.

References